Come trovare l'area di un triangolo isoscele

Matematica e geometria in particolare, secondosondaggi di scolari, una delle lezioni più non amate, e tutto perché ti fanno imparare un numero enorme di formule che nella vita il 90% degli attuali adulti non ha trovato applicazione pratica. Ma, per un minuto, impariamo le formule, risolviamo i problemi, facciamo equazioni non per il fatto che possono esserci utili nella vita, ma perché sviluppano il pensiero e la logica. Persino gli antichi saggi greci affermavano che l'intelletto umano può essere misurato dalla conoscenza delle scienze matematiche. E poiché hai deciso di familiarizzare con l'applicazione delle formule per un triangolo isoscele, ci prendiamo in mano e leggi l'intero articolo.
Prima di iniziare a rispondere alla domanda come trovarel'area di un triangolo isoscele e vai alla parte pratica dell'articolo, dove vengono fornite formule e calcoli, denotiamo il concetto stesso per noi stessi. Un triangolo isoscele è un triangolo in cui due dei tre lati sono uguali in lunghezza, che sono chiamati lati laterali. Nel caso di un triangolo regolare, in cui tutti i lati sono uguali, viene anche considerato isoscele, ma viceversa, quando un triangolo isoscele viene considerato corretto - è falso.
I lati del triangolo dovrebbero essere designati, lo faremo in questo modo, come mostrato nella figura sotto, dove: a - lati, b-base e altezza-h.
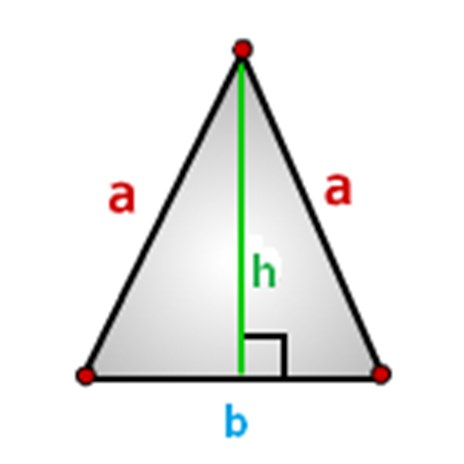
Come calcolare l'area di un triangolo isoscele, formule.
Dopo aver fatto la notazione di altezza, lati e angolazione, possiamo iniziare a risolvere il problema.
Per cominciare, determineremo ciò che sappiamo.
Se l'altezza e il fondo - quindi la formula classica (* - segno di moltiplicazione):
S = ½ * b * h
Sostituiamo, ad esempio, i numeri in cui: h = 16, b = 18, otteniamo quanto segue:
S = ½ * 18 * 16 = 9 * 16 = 144;
L'area di un triangolo isoscele è S = 144 cm2
Ci sono altre formule che ci aiuterannoin come conoscere l'area di un triangolo isoscele. Una di queste formule è il metodo di Heron. Non scriviamo una formula complessa, prendiamo, per una base, una riduzione:
S = ¼ b √4 * a2-b2
È chiaro che b è la base e - lati uguali. La formula è adatta nel caso in cui l'altezza h non sia nota.
Sostituendo i valori, sia a = 6, b = 3, otteniamo quanto segue:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Puoi usare per calcolare l'area uguale ai lati del triangolo e l'angolo tra i lati:
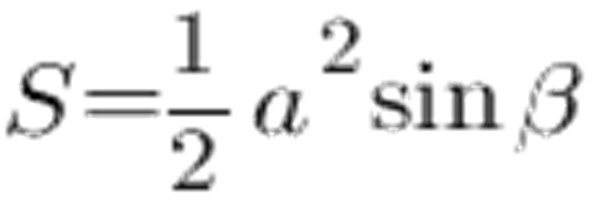
Secondo la tabella del seno, l'angolo a 45 ° equivale a 0,7071, il lato a e lo lascia 6 cm, otteniamo quanto segue:
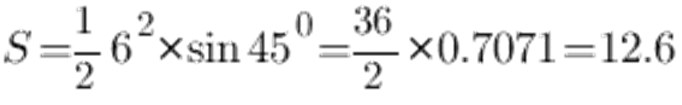
Di conseguenza, l'area di un triangolo isoscele è 12,6 cm2.
Ci sono anche modi per calcolare l'area, inclusoincluso nel caso di un triangolo isoscele, ma sono piuttosto complicati e non si applicano ai calcoli "elementari", come quelli sopra, nella nozione di matematica complessa. E non vale la pena parlare di cose che anche gli insegnanti con esperienza non capiranno.
Quindi, puoi tirare un sospiro di sollievo, su questoun piccolo corso di geometria per trovare l'area di un triangolo isoscele sarà considerato completo e la conoscenza ottenuta come risultato della lettura dell'articolo viene appresa da "cinque".














